The last blog was the final entry talking about the aspects of blobs that cause problems to be difficult. Now, we’re going to talk about the aspects of arrows (III) that cause problems to be difficult.
Continuous functions are a familiar concept to those who have taken calculus before. With the diagrams we’ve been using, the function in this context is going to be our arrow and the input/output spaces are going to be our input and output blobs. The gist of a continuous function is that a small change in the input that you feed a function is going to result in a small change in the output that the function produces.
This means that you’re going to need a blob that has sufficient structure to decide whether or not the arrow leaving it is continuous or not. Blobs that are metric spaces and blobs that are topologies are both going to be able to support a notion of continuous functions/arrows.
Why do continuous functions matter?
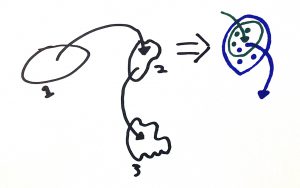
The issue is that most systems we encounter are not going to be composed of a single input blob, single arrow, and single output blob. The above system is composed of three blobs and two arrows. This means that the second blob actually represents two separate blobs: an output blob from the previous arrow and a valid input blob for the next arrow.
If all arrows in the system are continuous arrows, then predictability of the system is going to be increased. Once you understand the initial condition of the system and the corresponding final condition of the system, you can rest assured that any small variations in the input of the system will result in a final condition that is “close” to the final condition that you are familiar with. Small changes in the input will result in small changes in the output. This type of system will be easy to form intuitions about.
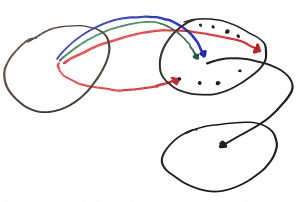Discontinuous arrows are problematic for two reasons. The first reason is that because small changes in input may result in large changes in output, the system’s final condition will be very difficult to predict based off of the initial condition of the system. Forming an intuition of how the system works will be very difficult or impossible. The worst case scenario being that in order to understand the system you have to know how every possible initial condition maps to its corresponding final condition. Depending on how big the blob of initial conditions is, this mapping may be radically impractical to impossible to build.
The second reasons is that some of blobs in the system are going to have holes. If you have a continuous arrow, then once you understand the general behavior of the arrow you will also understand which inputs are dangerous. Inputs that have outputs that reside near holes for the next blob need to be handled with caution because a slight change could result in the system entering an invalid state. However, inputs that have outputs that reside far from holes can safely be used as there exists a margin of safety.
With discontinuous arrows, you never know when a small change in the input is going to result in the system ending up in an invalid state. Any change may result in the entire system crashing, so it’s going to be very difficult to deal with this sort of system.
Continuous functions result in problems that are easy to form intuitions for. Discontinuous functions result in problems that are fragile and hard to understand.
Next let’s explore how all of the arrows in a system and how they relate to blobs can make things difficult.
