Our previous posts were talking about the aspects of our blobs (**I **and II). Now we’re going to transition to talking about the aspects of the contents inside of our blobs that indicate a problem that is more difficult to deal with.
Consider a method that takes an integer as input, but that will only behave reasonably if it is a certain type of integer.
public double Method( int i )
{
return 100 / ( i - 2 );
}This is why when we first talked about the input blob I, we also talked about it as the valid input blob. Where “valid” meant something along the lines of “value that allows the system to continue healthy functioning”. In the method above, we see that any integer can be used except the integer 2. In this context the integer 2 would be invalid input because it would cause Method to throw a division by zero exception.
The problem is inexact types
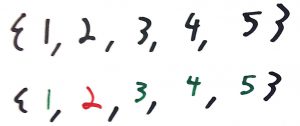
With Method above the problem is that the method reports to us that integers are valid inputs, but the reality is that what the method actually means is that all integers are okay besides the integer 2. If a software engineer was using this method, then additional information is going to have to be learned, retained, and considered with every usage. A method that correctly reports what valid input means is going to be easier to work with.
The problem is that now you have unnatural data to deal with
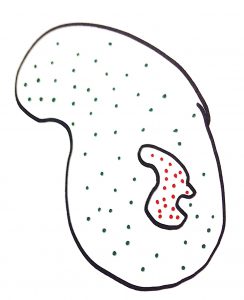
Just having more exact types isn’t necessarily going to make the problem easier to deal with. The reason why nearly every programming language has an integer type is because it represents a very natural set of values that we see over and over again in different domains. Because integers are a reoccurring theme in many domains, it’s easy for people to conceptualize them. They have a lot of experience working with the idea. If you consider the blob above you notice kind of an amorphous shape embedded inside of it that contains invalid inputs to the system. What are the chances that this new set of values (everything green except the funny shape full of red) is something that very many people have a natural intuition of how to deal with. Probably not likely and it only gets worse.
Invalid data sets can be arbitrarily bad to work with
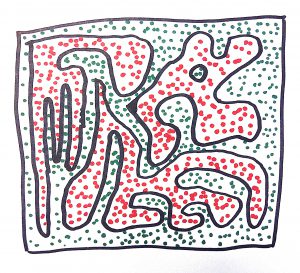This diagram shows what could be a very easy-to-work-with two dimensional data set. Unfortunately, it’s filled with invalid portions that have no rhyme or reason. Even if you could build a data structure that only allowed correct values of this data set to be constructed, understanding how to correctly construct a value would be time consuming and frustrating.
Also consider that the data sets we’ve been talking about so far are only one or two dimensional. Imagine a five dimensional blob that has four dimensional invalid spaces that float around inside of it. I’m not sure I can imagine it, but we potentially have to deal with problems like this.
Topological Hole
In an earlier blog entry, I said that we really want these blobs to be metric spaces (or at the very least a topological space). This is partially because this type of space allows our intuitions something to work with that is familiar. But having a blob be at least a topological space provides us with a mathematical tool to try and define the invalid region that this post is all about. In topology it’s called a hole and it’s a well defined concept that I believe we can apply to the analysis of problems. In the above examples it’s pretty easy to say that some of them feel complicated. But it would be a lot more objective to be able to topologically identify the number and “shape” of the invalid input holes in our blobs. This is especially important when dealing with higher dimensional blobs where it’s going to be very difficult to visualize what we’re looking at. Having a mathematical tool should make identifying the aspects of what we’re encountering possible.
Make sure that your Valid Input Blob has minimal (and simple) holes
Next we can talk about a way to try to deal with blobs that have a lot of holes.
